A Simple analysis of Schema Theorem and
Siddhartha K Shakya
School of computing, The
Abstract:
From the early stages of development of Genetic Algorithm (GA) theory, the Schema Theorem and the Building Block Hypothesis have been the dominant explanation for the working process of GA. In this article we will first look at the Schema Theorem from the point of view of one of the early pioneers of GA, D. Goldberg [Goldberg 89] and explain how Schemata Theorem helps to understand the GA behaviour. In the second part of the article we will look on Royal Road (RR) functions specially designed to contradict the Building Block Hypothesis. We will explain RR function from point of view of one of its designers Melanie Mitchell [Mitchell 98] and analyse the poor performance of GA on such type of functions.
Part 1: Schema Theorem and its
contribution towards understanding GA behaviour
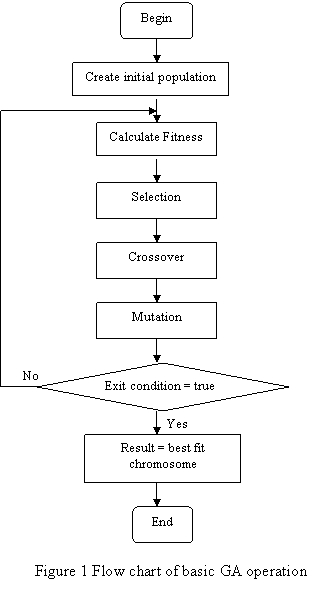
The operation of GA is straight-forward. We start with a random population of n strings where each individual string in the population is known as a Chromosome and has its own fitness value. We copy strings with some bias towards the best i.e. high fit chromosomes are more likely to be copied. This process of copying strings is known as selection process. We then crossover the best strings i.e. mate best strings and partially swap substrings. Finally mutation process takes place where we mutate an occasional bit value of resulting string for good measure. Flow chart presented in figure 1 describes the basic GA.
Now let’s model the operation of GA in terms of mechanics of natural selection and natural genetics. As stated above, chromosomes in a population with high fitness are more likely to be selected for the reproduction and consequently likely to produce more offspring in the next generation were as the less fitted chromosomes are more likely to die. This characteristic of GA models the concept of survival for the fittest. Crossover plays the role of mating process between parent chromosomes such that the reproduced child will have function of both of its parents. The mutation process represents the error in the reproduction process, occurrence of which may differ child from its parents.
To analyse the behaviour of GA, the notion of schema has been introduced. Schema can be defined as a string containing all similar bits (defined bits) among highly fit chromosomes in a population, where non similar bits (non defined bits) are represented as ‘*’ (Don’t care) symbol. Let’s see an example.
The chromosomes in a current generation containing all defined bits of a schema are known as instances of that particular schema. Figure 2 shows a schema with two defined bits and two non defined bits. The possible instance of the schema is shown in Figure 3.
Figure 3 Set of 4 bit chromosome matching schema shown
in figure 2
Schema provides the basic means for analyzing the net effect of reproduction and genetic operators on Building Block contained within population [Goldberg 89]. The concept: important similarities among highly fit strings can help guide search, lead to the concept of schema (schemata in plural).
Given a current generation of chromosomes, the Schema Theorem helps to predict the number of instances of schema in the next generation [Goldberg 89]. Let’s give explanation to the above statement.
As we know that the probability of selection of a chromosome is proportional to its fitness, we can calculate the expected number of instances of a chromosome in next generation, which can be written as
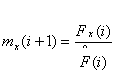
Where,
: Number of instances of chromosome x in i+1 generation
: Fitness of
chromosome x in i generation
: Average fitness of chromosome in i generation
Similarly by knowing chromosomes matching the schema in current generation, we can calculate the number of instances of that schema in next generation. It can be written as:
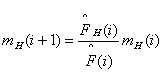--------------(1)
Where,
: Number of instances of schema H in i+1 generation
: Number of instances of schema H in i generation
: Average fitness
of chromosomes containing H in i generation
: Average fitness of chromosomes in i generation
Equation 1 clearly states that, particular schema grows as the ratio of the average fitness of the schema to the average fitness of population, i.e. Selection process allocates increasing number of samples to above average fit schemata.
However, selection process alone does nothing to promote exploration of new regions of the search space. i.e. it only selects the chromosomes that are already presented in current generation. To avoid such case, crossover and mutation operators are needed. But crossover and mutation both can create schemata as well as can destroy them. Schema Theorem considers only destructive effect of crossover and mutation, i.e. the effect that decreases the number of instances of the schema to be occurred in next generation.
The probability that the schema H will survive after crossover can be expressed as
Where:
: Crossover
probability
: Chromosome
length
: Defining length which is calculated as the
distance between outermost
defined bits of schema H . If crossover takes place within defining
length, the probability that the schema H will be disrupted will
increase.
Now let us consider the destructive effect caused by the mutation. The probability that the schema H will survive after mutation can be expressed as
Where,
: Mutation
probability
n : Order of schema H , which is equal to the number of defined bits in
schema H.
Here 
represents the
probability that an individual bit will not be mutated.
So taking to account the destructive effect of crossover and mutation, equation (1) can be reformulated as
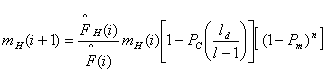
--------------(2)
Equation (2) is known as the Schema Theorem, which gives lower bound on the expected number of schemata on next generation.
Let us analyse the individual
component of schema theorem in more detail. Looking on the formula which calculates
destructive effect of crossover, we see that if << l, the
probability that crossover will take place within is low. So it is clear that the probability of survival of
schemata after crossover is higher for the short schemata. Similarly looking on
formula which calculates destructive effect of mutation, we see that if value
of n is low, the probability that the
mutation will take place within defined bits of schema H will be lower. So it is also clear that survival after mutation
is high for the low ordered schemata. Finally we can see that if >, the probability of the schema H being selected for the next generation is high, which means the
probability of selection for reproduction is high for above average fit
schemata. Consequently we can make the conclusion that the short, low order,
above average fit schemata receives increasing samples in subsequent
generations. These short, low-order, above average fit schemata are known as Building
Blocks. Building Block Hypothesis states
that GA seeks the near optimal performance through the juxtaposition of these
Building Blocks [Goldberg 89].
It is important to understand that the genetic algorithm depends upon the recombination of Building Blocks to seek the best point. However, if the Building Blocks are misleading due to the coding used or the function itself, the problem may require long waiting times to arrive at the near optimal solution. We will describe this in next part of the article.
Part 2:
In the previous part, we have discussed the Schema Theorem and its impact in understanding the behaviour of GA. We showed how schema theorem leads to the Building Bock Hypothesis. However, as shown by some later researches GA actually process Building Blocks in a way that does not always satisfies Building Block Hypothesis. In this part of the article we will discuss a GA called Royal Road (RR) specially designed to show the limitations of Building Block Hypothesis.
The Schema Theorem, by itself, addresses the positive effect of selection allocating increasing samples of schemas with observed high performance, but only the negative aspect of crossover [Mitchell 98]. i.e. it only takes in account the lower bound of survival of schema after crossover takes place. However, many of the researchers have seen crossover as the major source of the search power of GA. The Schema Theorem does not address the question of how crossover works to recombine highly fit schemas. The Building Block Hypothesis states that crossover combines short, low order highly fit schemas into increasingly fit candidate solution but does not describe how this combination takes place [Mitchell 98].
To investigate the behaviour of GA in more detail, special class of fitness function called Royal Road (RR) has been introduced. RR functions were meant to capture the essence of Building Blocks in an idealized form.
=
11111111******************************************************** 
= 8
= ********11111111************************************************
= 8
=
****************11111111**************************************** 
= 8
=
************************11111111******************************** 
= 8
=
********************************11111111************************ 
= 8
= ****************************************11111111****************
= 8
= ************************************************11111111********
= 8
= ********************************************************11111111 
= 8
=1111111111111111111111111111111111111111111111111111111111111111
= 64
Figure 4: Schemata definition in Royal Road Function
The Building Block Hypothesis
suggests that the short, low order highly fit schemas are combined together to
create more fit schemas and they are again combined to create even more fit
schemas and so on. Schemata 
in RR function as
shown in figure 4 satisfies the criteria of short defining length and
low order as stated by the Building Block Hypothesis. The optimum string has been divided into eight different
schemas with equal fitness 
= 8. The fitness of
the optimum string is sum of fitness of
all the schemas i.e. = 64.
Given the Building Block Hypothesis
one might expect that the GA will find the optimum string very easily and fast
creating a kind of
Experimental analysis showed that the reason behind such poor performance of GA in RR functions was because of “hitchhiking”. Once the higher order schemas were found, its high fitness allowed it to get reproduced increasingly in the next generation and spread out quickly in the population. However, together with the defined bits (ones) in highly fit schemas, the non defined zeros in other position in the string has also been hitchhiked and spread out in the population, which prevented and slowed the occurrence of the certain schemata in the population especially of those with the defined bits closer to the non defined zero bits of the highly fit schemata. Even if these certain schemata would occurred in some point, there would be low probability that it would survive for the next generation as other high fit schemata would be dominating the selection process. Consequence of this kind of behaviour of GA made it take long time to get the optimum solution.
From these experimental results, we can conclude that hitchhiking seriously limits the performance of GA by restricting the schemata sampled at the certain loci as well as it provides evidence that for certain kind of problems, Building Block Hypothesis can not be applied as stated previously.
References:
- David E. Goldberg. 1989. Genetic Algorithms in search, optimization and machine learning. Addison-Wesley.0-201-15767-5
- Melanie Mitchell. 1998. An Introduction to genetic Algorithm. MIT Press. 0-262-113316-4(HB)